Context Free Grammar
What is the Context Free Grammar?
A context-free grammar (CFG) consisting of a finite set of grammar rules is a quadruple (N, T, P, S) where,
● N is a set of non-terminal symbols.
● T is a set of terminals where N ∩ T = NULL.
● P is a set of rules, P: N → (N ∪ T)*, i.e., the left-hand side of the production rule P does have any right context or left context.
● S is the start symbol.
Examples
1. Exampe
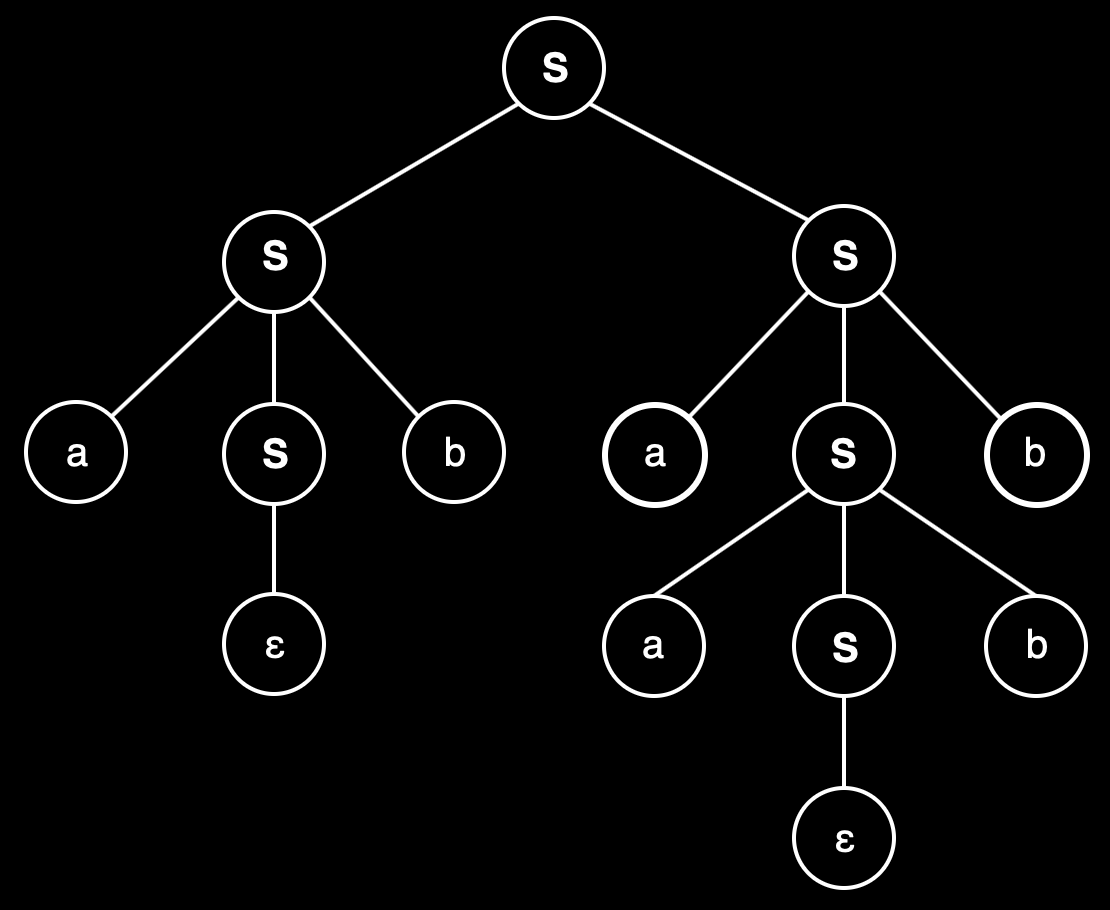
▶︎ Let a CFG {N,T,P,S} be
▶︎ N = {S}
▶︎ T = {a, b}
▶︎ Starting symbol = S
▶︎ P = S → SS | aSb | ε
One derivation from the above CFG is “abaabb”
S → SS → aSbS → abS → abaSb → abaaSbb → abaabb
2. Example
▶︎ The grammar ({A}, {a, b, c}, P, A), P : A → aA, A → abc.
2. Example
▶︎ The grammar ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
3. Example
▶︎ The grammar ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε
Context Free Grammar to Parse Tree
Generation of Derivation Tree
A derivation tree or parse tree is an ordered rooted tree that graphically represents the semantic information a string derived from a context-free grammar.
Representation Technique
● Root vertex : Must be labeled by the start symbol.
● Vertex : Labeled by a non-terminal symbol.
● Leaves : Labeled by a terminal symbol or ε.
If S → x1x2 …… xn is a production rule in a CFG, then the parse tree / derivation tree will be as follows :
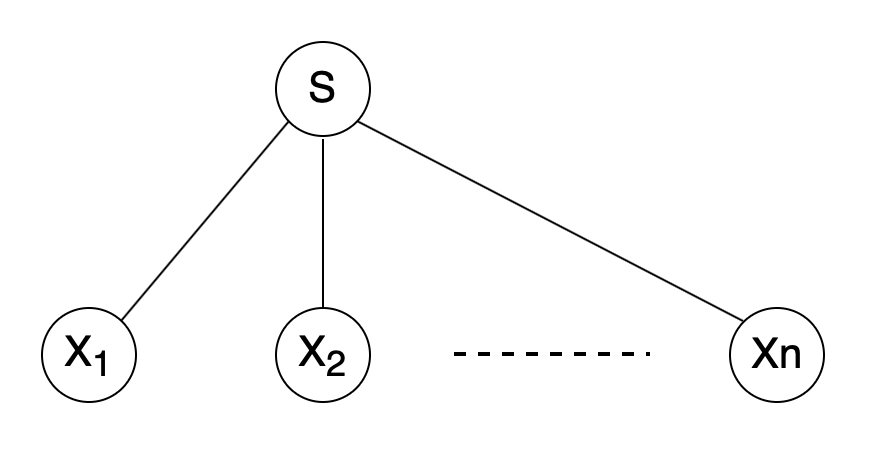
There are two different approaches to draw a derivation tree :
1. Top-down Approach :
▶︎ Starts with the starting symbol S
▶︎ Goes down to tree leaves using productions
2. Bottom-up Approach :
▶︎ Starts from tree leaves
▶︎ Proceeds upward to the root which is the starting symbol S
Sentential Form and Partial Derivation Tree
A partial derivation tree is a sub-tree of a derivation tree/parse tree such that either all of its children are in the sub-tree or none of them are in the sub-tree.
Example
If in any CFG the productions are :
S → AB
A → aaA | ε
B → Bb| ε
the partial derivation tree can be the following :

If a partial derivation tree contains the root S, it is called a sentential form. The above sub-tree is also in sentential form.
Leftmost and Rightmost Derivation of a String
● Leftmost derivation : A leftmost derivation is obtained by applying production to the leftmost variable in each step.
● Rightmost derivation : A rightmost derivation is obtained by applying production to the rightmost variable in each step.
Example
Let any set of production rules in a CFG be
X → X+X | X*X | X | a
over an alphabet {a}.
The leftmost derivation for the string "a+a*a" may be :
X → X+X → a+X → a + X*X → a+a*X → a+a*a
The stepwise derivation of the above string is shown as below :

The rightmost derivation for the above string "a+a*a" may be :
X → X*X → X*a → X+X*a → X+a*a → a+a*a
The stepwise derivation of the above string is shown as below :

Notes
Used Automata theroy book as reference
All photos are drawn with drow.io.
The following websites used as reference "website 1" and "website 2"
Uses W3.CSS Template